
Archimedes developed a technique to find areas and volumes called ‘the method of exhaustion’ that came close to the ideas used in modern calculus.

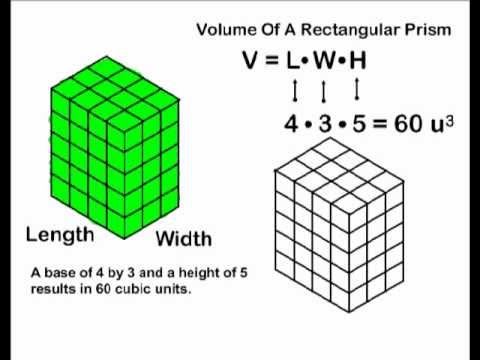
He also derived the formulas for the volume and surface area of the sphere. 287 − 212 BC) approximated the area of a circle using inscribed polygons and found very good approximations to π. The ancient Greeks were the first to systematically investigate the areas and volumes of plane figures and solids.ĭuring the Hellenistic Period, the great mathematician Archimedes (c. For example, trapezium (despite the Latin ending) comes from the Greek word for table, while prism is derived from a Greek word meaning to saw (since the cross-sections, or cuts, are congruent), also the word cylinder is from a Greek word meaning to roll. Many of the names of the figures and solids whose area and volume we have found come from the Greek. Where A is the area of the polygonal base and h is the height when the prism is sitting on its base. Since any polygon can be dissected into triangles, the volume of any prism with polygonal base is the area A of the polygonal base times the height h, that is Volume = area of triangular cross-section × perpendicular height = Ah. Thus the volume of a triangular prism is given by The volume of each of the 1 cm layers is half the volume of the corresponding rectangular prism, i.e. Similarly we can complete the triangular prism to form a rectangular prism. We saw earlier that we can complete an acute-angled triangle to form a rectangle with twice the area. We can cut the prism into layers, each of length of 1 cm. Suppose we have a triangular prism whose length is 4 cm as shown in the diagram. In a triangular prism, each cross-section parallel to the triangular base is a triangle congruent to the base. Students should understand why the formulas are true and commit them to memory. In this module we will use simple ideas to produce a number of fundamental formulasįor areas and volumes. In physics the area under a velocity-time graph gives the distance travelled.

Medical specialists measure such things as blood flow rate (which is done using the velocity of the fluid and the area of the cross-section of flow) as well as the size of tumours and growths. It is important to be able to find the volume of such solids. Packet (with the base at the end) is an example of a triangular prism, while an oil drum Similarly, solids other than the rectangular prism frequently occur. The view consists of two trapezia and two triangles.

Consider, for example, this aerial view of a roof. While rectangles, squares and triangles appear commonly in the world around us, other shapes such as the parallelogram, the rhombus and the trapezium are also found. Builders and tradespeople often need to work out the areas and dimensions of the structures they are building, and so do architects, designers and engineers. Calculating areas is an important skill used by many people in their daily work. S = \dfrac = 12Ĭalculating the volume of a prism can be challenging, but with our prism volume calculator and formula, it's easy to find the volume of any prism.The area of a plane figure is a measure of the amount of space inside it. Here are some examples of finding the volume of a prism using the formula: Example 1įind the volume of a rectangular prism with a base of length 5 cm and width 8 cm, and a height of 10 cm.įind the volume of a triangular prism with a base of height 4 cm and base width 6 cm, and a height of 12 cm.


 0 kommentar(er)
0 kommentar(er)
